(1) Ako legneš u 8 sati i probudiš se u 9 sati, koliko si sati spavao ?

(2) U kutiji imaš jednu šibicu i ulaziš u mračnu prostoriju u kojoj se nalazi plinska

      peć i peć na drva. Što ćeš prvo upaliti ? 

(3) Postoji li u Americi 29.02. ? 

(4) Neki mjeseci imaju 30 dana, neki 31 dan. Koliko ih ima 28 dana?

(5) Što piše na kovanici od deset kuna ? 

(6) Ako pijetao snese jaje na hrvatsko-slovenskoj granici čije je jaje? 

(7) Dobiješ tri tablete, svakih pola sata popiješ po jednu. Koliko ti vremena

      treba da popiješ sve tri ?

(8) Što je bilo u Kini nakon 1956. godine ? 

(9) Sanjaš da si u tunelu, s jedne strane dolazi zmaj, a s druge vlak. Što će se 

     dogoditi na kraju ? 

(10) Avion se srušio na hrvatsko-mađarskoj granici. Gdje će pokopati ranjenike ?

(11) Što će se dogoditi, ako bijeli kamen padne u Crveno more ? 

(12) Ja sam ti sin, a ti mi nisi otac. Tko si mi ti ?   

(13) Šest automobila je zaustavljeno na hrvatsko-turskoj granici. Za pregled jednog

       automobila treba 10 minuta. Koliko treba vremena za pregled svih vozila ? 

(14) Ako danas u podne pada kiša, može li za 36 sati biti sunčano ?

(15) Čovjek počini samoubojstvo, dođu dvije žene na sud od kojih jedna ima 

       potpuno bijelu haljinu, a druga ima krvavu mrlju na haljini. Koja ga je ubila ?

(16) Koje životinje mogu skočiti više od ormara ?

(17) Postoji li broj čiji je broj slova u njegovom imenu jednak tom broju?

(18) Zašto Ljubica ima crvene gumbe na kaputu, a Ljiljana plave ?

(19) Zašto bijele ovce popasu više trave od crnih ?

(20) Mladen je došao u trgovinu. Objasnio je trgovcu što treba, a trgovac 

        mu odgovori: '' Za jedan treba  10 kuna, za pet 10 kuna, za petnaest

       20 kuna, za pedeset 20 kuna, za sto trideset kuna, a za dvjesto isto 30

       kuna.'' Što kupuje Mladen ?

(21) Koja riječ od četiri slova ima pet O ?

(22) Koja riječ kad se čita s lijeva na desno ima k, a kad se čita s desna na lijevo

        nema k ?

(23) Djed Tomislav je imao u krletki tri papagaja i poklonio ih svojim unucima

       Darku, Mirku i Slavku. Svaki je unuk dobio jednog papagaja, a jedan je 

       papagaj ostao u krletki. Kako je to moguće?

J K J K J K J K J K J K J K J K J

I još malo (različito i prigodno…)

Bio jedan stari beduin. On je imao tri sina. I kad je došlo vrijeme da stari beduin umre on reče svojim sinovima: ”Najstariji će dobiti 1/2 nasljedstva, srednji će dobiti 1/3 nasljedstva, a najmlađi će dobiti 1/9 nasljedstva”. I tako je i bilo: stari beduin umro, a nasljedstvo se raspodijelilo. No, ostalo je 17 deva. A najstariji hoće svoju 1/2, srednji hoće svoju 1/3, a najmlađi hoće svoju 1/9. No,17 se ne može podijeliti na 1/2, 1/3 i 1/9. Te oni odu do mudraca i kažu u čemu je problem. I mudrac kaže ovako: ”Ja ću vam dati još jednu devu, a vi kad se raspodijelite ćete meni vratiti ostatak”. Oni su sad imali 18 deva. najstariji je dobio 1/2 tj. 9 deva, srednji je dobio 1/3 tj. 6 deva, a najmlađi je dobi 1/9 tj. 2 deve. Od 18 su oduzeli 17 jer je 9+6+2=17. I tako je ostala jedna deva koju su vratili mudracu.

(1)      Pilići i zečevi krenuli su na Uskršnju misu. Sakupili su se u dvorištu. Danijel, koji se već vraćao s jutarnje mise, izbrojao je da pilići i zečevi imaju ukupno 40 nogu i 15 glava. Koliko je bilo pilića, a koliko zečeva ?

(2)     Matko Zbrojić si je kupio knjigu ''Uskršnji običaji''. Za označavanje stranica knjige, od prve do posljednje, upotrijebljeno je ukupno 570 znamenaka. Koliko Matkova nova knjiga ima stranica ?

(3)     Pilići krenuše na put. Jedan pilić ide ispred dva pilića, jedan pilić ide između dva pilića, a jedan pilić iza dva pilića. Koliko je pilića krenulo na put?

(4)     Članovi crkvenog zbora odmarajući se nakon jutarnje mise na Uskrs uočili su da svaki njihov član ili ima brkove ili nema kosu, a točno dvojica među njima su brkonje bez kose. Petina ukupnog broja nije brkata, a četvrtina nema ni vlasi na glavi. Odredite koliko je pjevača u crkvenom zboru.

(5)     U svakom kutu sobe nalazi se jedan bijeli zec, a nasuprot svakome bijelome zecu su tri bijela zeca. Koliko je zečeva u toj sobi ?

(6)     Martina u dvorištu ima tri kokoši. Jedna kokoš i pol snesu tri i pol jaja u pola dana. Koliko će Martina dobiti jaja od tri kokoši u tri dana? 

(7)     Marko je krenuo na sajam i ponio je točno sto kuna. Trebao je za Uskrs kupiti zečeve, piliće i jaja. Marko je kupio ukupno sto komada (sveukupno zečeva, pilića i jaja bilo je sto). Za jednog zeca Marko je izdvojio 10 kuna, za pilića 5 kuna, a za jaje pola kune. Koliko je Marko donio kući zečeva, pilića i jaja ?

1. Koji broj treba stajati umjesto upitnika ?

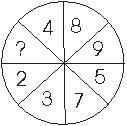
 * R: 4, zbroj nasuprotnih je 11 *

2. Andrea je starija od Barbare i Toma. Tom je stariji od Donne. Bob je mlađi od Barbare, ali je stariji od Donne. Bob je mlađi od Toma. Andrea je mlađa od Felicije. Poredajte ih od najstarijeg do najmlađeg.

* R: Felicia, Andrea, Barbara, Tom, Bob i Donna *

3. Koji broj treba doći na mjesto upitnika ?

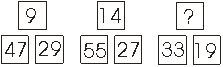
* R: 33 – 19 = 14, 14 : 2 = 7 *

4. Ivan i Marko dijele određenu svotu novaca u omjeru 4:5. Na kraju Marko ima 60 kuna. Koliko su novca imali ?

* R: 5x =60, x = 12, zajedno su imali 108 kuna *

5. Koji broj nastavlja niz ? 1, 10, 3, 8, 5, 6, 7, 4, 9, ?

* R: dva niza 1, 3, 5, 7, 7 / 10, 8, 6, 4, 2 *

6. Koji broj treba stajati na mjestu upitnika ?

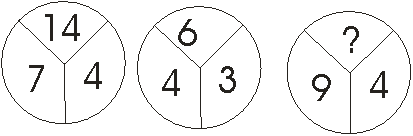
* R: pomnožiti donje brojeve i podijeliti s 2, rješenje je 18 *

7. Čovjek pretrči određeni put brzinom 6 km/h, a isti taj put propješači brzinom od 4 km/h. Koja je njegova prosječna brzina ?

*R: 4.8 km /h ; za put dug 6 km kad trči treba mu 1 h, kad hoda treba mu 1.5 h, znači za put od 12 km mu treba 2.5 h *

8. Koji broj treba stajati na mjestu upitnika ?

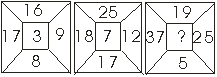
* R: rješenje je 2; zbroj gornjeg i donjeg broja podijeliti s razlikom brojeva koji su lijevo i desno *

9. Koji broj treba stajati na mjestu upitnika ?

*R: rješenje je 7; u svakome retku i stupcu zbroj naizmjeničnih polja je jednak *

10. Ivan ima 6 kuna više od Marka, ali da Marko ima tri puta više nego sada, imao bi 6 kuna više od njihove sadašnje zajedničke svote. Koliko novaca ima Ivan ?

*R: Ivan 18, Marko 12 *

11. Koji broj treba stajati na mjestu upitnika ?

*R: 10; pomnožiti prvi i treći broj, oduzeti drugi i dobije se četvrti *

12. Koji broj treba stajati na mjestu upitnika ?

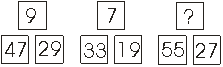
* R: 14; oduzeti donje brojeve i podijeliti ih s 2 *

13. Radnik je primio 20 $ za svaki dan svoga rada, ali je prema uvjetima iz ugovora izgubio 30 $ za svaki dan koji nije radio. Nakon 30 dana je otkrio da je izgubio onoliko novaca koliko je i zaradio. Koliko dana je radio radnik ?

* R: radio je 18 dana *

14. Moj sin ima isti broj godina kao ja kad se okrenu znamenke. Red godinu dana bio sam dvostruko stariji od svog sina. Koliko godina ima sin ?

* R: otac 73, sin 37 *

15. Koji broj treba stajati umjestu upitnika ?

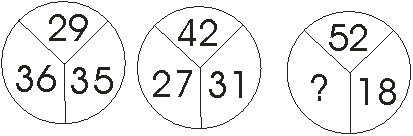
* R: rješenje je 30; u svakom krugu zbroj brojeva je 100 *

MATEMATIKA  I  VALENTINOVO

iz računalnog programa Winplot povodom Valentinova

ZA  OPROŠTAJ  OD  ŠKOLSKE  GODINE...

1.           da

2.           ne (6)

3.           da (bukva, klen)

4.           da (IV)

5.           ne (4)

6.           (c) – 42 m

7.            (b) – 9 m

8.           (a) – 6 dana

9.           (c) - 5 puta

10.        (c) – 156 m

11.        list

12.        1 min

13.        2*12 – 5 = 19

14.        15*5, 25*2

  15.

 s  �  ¦ ZZANIMLJIVI  ZADACI  I  PITANJAA  &  J  !

(1)  Otac je stariji od sina 3 puta, a sin je stariji od sestre 3 puta. Koliko je godina ocu, ako zbroj njegovih i kćerkinih godina iznosi 50 ?

(2)  Zbroj dva broja iznosi 330. Kada se većem broju odbije s desne strane nula, ti brojevi postaju jednaki. Koji su to brojevi ?

(3)  Kada je pješak prešao polovinu puta i još 2 km, ostalo mu je da prijeđe četvrtinu puta i još 6 km. Kolika je duljina puta ?

(4)  Četrdeset i šest putnika se prevozi u 10 čamaca preko rijeke, od kojih su neki po 4, a neki po 6 sjedišta. Koliko je bilo čamaca svake vrste, ako su svi bili puni ?

(5)  Na šahovskom turniru sudjelovalo je 7 šahista i svaki je sa svakim odigrao po jednu partiju. Koliko su oni partija odigrali ukupno ?

(6)  Koliko ima troznamenkastih brojeva koji imaju isto značenje bilo da se čitaju slijeva nadesno ili zdesna nalijevo ?

(7)  Pas je pojurio za zecom u trenutku kad se zec nalazio 30 m ispred njega. Pas čini skokove od 3 m, a zec od 2 m. Koliko skokova treba učiniti zec da bi sustigao zeca ?

(8)  Za numeriranje jedne knjige bilo je potrebno 1 128 brojaka. Koliko stranica ima ta knjiga ?

(9)  Broj pedeset pet izrazite s pet četvorki.

(10)                   Puž se penje na stup visok 10 m. Danju se popne 5 m, a noću se spusti 4 m. Koliko mu dana treba da se popne na vrh ?

(11)                   Pomoću dvije posude od 3 l i 5 l odmjerite iz vodovodne slavine u vrč 4 l vode.

(12)                   Koliko ima troznamenkastih brojeva ?

(13)                   U broju 4 673 942 treba izostaviti dvije brojke tako da broj koji ostane bude što je moguće: (a) veći, (b) manji.

(14)                   U kavezima se nalaze zečevi i fazani. Ove životinje imaju ukupno 35 glava i 94 noge. Koliko je fazana i zečeva ?

(15)                   Zadatak iz VIII. stoljeća... Čovjek mora preko rijeke prevesti vuka, kozu i kupus. U čamac se mogao smjestiti samo čovjek, a s njim ili vuk, ili koza, ili kupus. Ali ako ostavi vuka skozom, tada će vuk pojesti kozu; ako ostavi kozu s kupusom, tada će koza pojesti kupus, a u prisustvu čovjeka «nitko nikog ne jede». Čovjek je uspio prevesti preko rijeke vuka, kozu i kupus. Kako je on to uradio ?

RJEŠENJA

(1)   45 godina 

(2)   300 + 30 = 330 

(3)   32 km 

(4)   3 velika i 5 malih 

(5)   21 partija 

(6)   90 brojeva 

(7)   30 skokova 

(8)   412 Str 

(9)   44 + (4 : 4) = 55

(10)                     6 dana 

(11)                     napuniti 5 l i naliti u 3 l, ostaje 2 l (i još jednom) 

(12)                     900 

(13)                     a) 73 942   b) 43 942 

(14)                     12 zeca, 23 fazana 

(15)                     vuk ne jede kupus, zato se prvo preveze koza ostaju kupus i vuk). Čovjek se vraća po kupus i vozi ga preko. Ostavlja kupus i vraća se s kozom. Ostavlja kozu i prevozi vuka. Vraća se po kozu.